the bug that taught me more about PyTorch than years of using it

a loss plateau that looked like my mistake turned out to be a PyTorch bug. tracking it down meant peeling back every layer of abstraction, from optimizer internals to GPU kernels.

Expected to fix: my hyperparameters. Actually had to fix: PyTorch backend.

My training loss plateaued and wouldn’t budge. Obviously I’d screwed something up. I tried every hyperparameter combination, rewrote my loss function, spent days assuming I’d made some stupid mistake. Because it’s always user error.

This time, it wasn’t. It was a niche PyTorch bug that forced me through layers of abstraction I normally never think about: optimizer internals, memory layouts, dispatch systems, kernel implementations. Taught me more about the framework than years of using it.

I had a surprisingly fun time with this bug hunt and wrote up the whole investigation step-by-step, explaining framework internals as they become necessary to crack the case. If you enjoy debugging mysteries or find that tracking down bugs teaches you more than docs ever could, this might resonate. 🕵️‍♀️

Debugging post-mortems sometimes make me worry I wouldn’t have been smart enough to figure them out myself. So I structured this walkthrough to show the reasoning behind each step: what clues suggested each move, why I tested that hypothesis, why certain results pointed where they did. While the investigation took time and persistence, it didn’t require any particular expertise or wizardry— just observation and willingness to keep digging. I’ve included background knowledge exactly when you need it to understand the next step—think of it as an excuse to learn (or re-learn) PyTorch internals through a real problem. If you’d prefer to jump straight to reproducing the bug yourself, check out the minimal reproduction script and walkthrough on GitHub. Otherwise, join me on the investigation!

Table of Contents: 🤔 The Mystery: A Plateauing Loss…… 🔎 Isolating the Problem…… 💻 Device-Specific Differences…… ⌺ Tensor Memory Layouts…… 💔 Identifying the Broken Operations……. 🍎 Inside the Kernel Implementation…… 🕵️‍♀️ Case Closed

TL;DR - Just tell me the bug

The Bug: A PyTorch GPU kernel bug silently failed when writing to non-contiguous memory, causing my model’s encoder weights to freeze during training on Apple Silicon (MPS backend, PyTorch <2.4).

The Technical Details: PyTorch’s MPS (Apple Silicon GPU) backend had a kernel bug where addcmul_ and addcdiv_ operations silently fail when writing to non-contiguous output tensors.

Why It Caused the Training Plateau:

Encoder weights initialized as transpose of decoder → non-contiguous memory layout
Adam’s state tensors inherited this layout (exp_avg and exp_avg_sq became non-contiguous)
MPS kernels for addcmul_/addcdiv_ don’t handle non-contiguous outputs correctly
Results computed but written to temporary buffer instead of actual tensor
For the non-contiguous encoder’s Adam parameters, exp_avg_sq.addcmul_() doesn’t update → value stays zero, then the parameter update via addcdiv_ also fails → complete silent freeze

The Fix:

Adjust your code: Make weights contiguous at initialization
Upgrade PyTorch: Upgrade to PyTorch ≥2.4 (fixes addcmul_/addcdiv_)
(Complete fix) Upgrade your Operating System: Upgrade to macOS 15+ (native non-contiguous tensor support)

Current Status: Random operations (normal_, uniform_, etc.) still have this bug on macOS < 15 as of PyTorch 2.10 (I submitted a PR to fix this). Other MPS operations may be affected.

Reproduction: A minimal reproduction script & walkthrough is available at https://github.com/ElanaPearl/pytorch-mps-noncontiguous-bug.

The Mystery: A Plateauing Loss

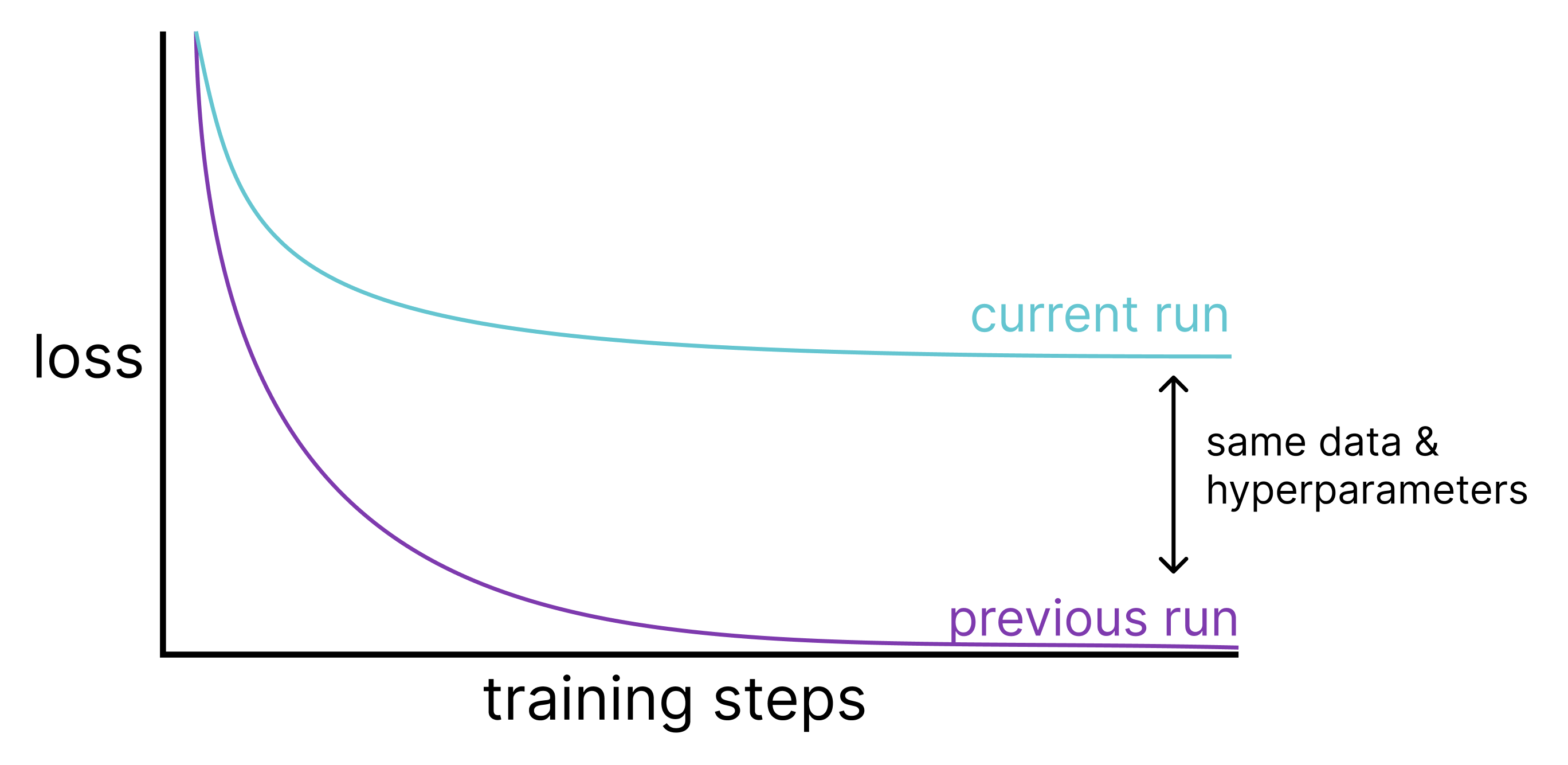
Training loss plateaued way too early. This felt like a standard hyperparameter issue- but I’d trained this same architecture on similar data with similar hyperparameters countless times and hit much lower losses.

What had changed? Those runs were months old. I tried reproducing them exactly, but couldn’t pin down the exact environment—the codebase had evolved through multiple projects, refactors, and dependency updates. Without a clean “before vs after,” I had to debug forward.

The architecture itself is straightforward: a two-layer sparse autoencoder (encoder –> sparse hidden layer –> decoder). However, it has some training quirks the could be potential culprits: the hidden layer uses TopK sparsity, where only the k largest activations remain (others are zeroed); the training process includes some manual gradient adjustments (gradient clipping for stability and modifications to decoder weight gradients); there’s an auxiliary loss term to encourage feature activation.

Even though I thought my initial hyperparameters were already well-tested, I tried everything: varied learning rates, tested different schedules, tried different k values and hidden dimensions, adjusted the auxiliary loss coefficients.

Nothing made a difference.

Meanwhile, my actual research sat on hold while I was stuck second-guessing everything: was my code broken? My data corrupted? And the creeping doubt- I’ve been doing ML for years, why can’t I make a simple two-layer autoencoder train properly?

The model was small enough that I was training on my MacBook (using the Apple Silicon GPU) and simple enough I could actually inspect every parameter. So after the standard checks turned up nothing, I started looking at the weights directly.

I visualized the weights at initialization and after the first few training steps. The decoder weights were updating- values shifting, gradients being applied, nothing crazy. But the encoder weights… weren’t updating at all. No NaNs, no suspicious patterns… they just… weren’t changing. They stayed exactly at their initialized values, down to the last decimal place.

Both layers participate in the same forward and backward pass. Why would one update and the other freeze completely?

Isolating the Problem

Are Gradients Flowing?

First check: are gradients even making it back to the encoder? The TopK sparsity should make gradients sparse—only the k activated features get gradients through backprop, the rest are zeroed. But maybe I messed up the implementation so that no encoder gradients flow at all? Or the manual gradient adjustments I was making somehow blocked everything?

After loss.backward(), the gradient statistics were:

	Encoder	Decoder
Max Grad	2.35e6	6.64e6
Sparsity	88.5% zeros	88.5% zeros

The encoder gradients were there- and they were pretty big (as intended for my dataset)! And they were sparse (majority zeros) which was also expected, but there were still plenty of non-zero gradients. So gradients are definitely being calculated.

Is It the Optimizer?

Since the gradients exist but weights aren’t updating, the optimizer must be doing something wrong. Testing with a simpler optimizer, stochastic gradient descent (SGD):

# Manual SGD update
with torch.no_grad():
    model.encoder.weight -= 0.001 * model.encoder.weight.grad
# Encoder weights change! ✓

# Torch SGD update
sgd_optimizer = torch.optim.SGD(model.parameters(), lr=0.001)
sgd_optimizer.step()
# Encoder weights change! ✓

# But with Adam...
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
optimizer.step()
# Encoder weights don't change! ✗

🤔

The issue is localized to Adam specifically! But why would Adam fail on the encoder but work perfectly on the decoder?

How Adam Works

To understand what might be breaking, I need to understand what Adam actually does differently from simple gradient descent.

Understanding Adam's Algorithm (click to collapse if familiar)

Two Problems with Vanilla SGD

Standard gradient descent (SGD) updates all parameters the same way:

# SGD: one learning rate for everything
param = param - learning_rate * gradient

This creates two fundamental problems:

Different parameters need different learning rates. Some parameters might consistently get gradients around 1000 while others get 0.01. With SGD’s fixed learning rate, you’re stuck: either you move too slowly on small gradients or you overshoot wildly on large ones.
The learning rate needs to change over time. Early in training, you want big steps to explore the space. Later, you need tiny steps to settle into a minimum. SGD requires manually decaying the learning rate on a schedule.

Adam’s Solution: Adaptive Learning Rates via Gradient Magnitude Tracking

Adam maintains two pieces of state per parameter and uses two hyperparameters to control how these states evolve:

State variables (initialized to zero for each parameter):

exp_avg: Running average of gradients (first moment)
exp_avg_sq: Running average of squared gradients (second moment)

Hyperparameters (typically beta_1=0.9, beta_2=0.999):

beta_1: Decay rate for first moment (momentum)
beta_2: Decay rate for second moment (gradient magnitude history)

Here’s the simplified algorithm:

Initialize state (done once per parameter)

exp_avg = zeros_like(param)
exp_avg_sq = zeros_like(param)
step = 0

Each training step:

# Update moments with exponential moving averages
exp_avg = beta_1 * exp_avg + (1 - beta_1) * grad
exp_avg_sq = beta_2 * exp_avg_sq + (1 - beta_2) * grad**2

# Update step count
# (It effectively starts at 1 to avoid division by zero in bias correction)
step += 1

# Bias correction
exp_avg_corrected = exp_avg / (1 - beta_1**step)
exp_avg_sq_corrected = exp_avg_sq / (1 - beta_2**step)

# Adaptive parameter update
param = param - lr * exp_avg_corrected / (sqrt(exp_avg_sq_corrected) + ε)

What Each Moment Does:

First moment (exp_avg): Smooths out noisy gradients by averaging recent directions—like momentum in physics. When gradients oscillate (+10, -10, +8, -9…), the positive and negative values cancel out, revealing there’s no consistent direction. Beta_1=0.9 means “keep 90% of old momentum, add 10% of new gradient.” This smoothed momentum is what gets multiplied by the learning rate in the parameter update: lr * exp_avg.
Second moment (exp_avg_sq): Tracks typical gradient magnitude for each parameter by averaging squared gradients. Squaring removes the +/- sign (both +10 and -10 become 100), preventing cancellation. Beta_2=0.999 means “keep 99.9% of magnitude history, add 0.1% of new squared gradient.” This magnitude normalizes the momentum-based update: lr * exp_avg / sqrt(exp_avg_sq). Parameters with consistently large gradients get their updates scaled down (large denominator), while parameters with small gradients get boosted (small denominator). This is how Adam achieves adaptive per-parameter learning rates.
Epsilon (ε=1e-8): Prevents division by zero.

Bias Correction:

Both moments start at zero, causing early estimates to be biased toward zero. The correction factor (1 - β**step) provides a large boost early to counteract this, effectively “warming up” the optimizer over the first ~1000-3000 steps. As training progresses, the correction approaches 1 and has negligible effect.

The second moment works similarly. Without correction, exp_avg_sq would be only 0.1% of gradient² at step 1, but bias correction restores it to the full value.

For a deeper dive into Adam’s design and intuition, as well as other optimizers that use momentum and adaptive learning rates (RMSprop, AdaGrad, etc.), check out Stanford’s CS231n notes on optimization.

Knowing what Adam should be doing, let’s look at the state it’s maintaining (those exp_avg and exp_avg_sq tensors that track momentum and variance) to see what it’s actually doing.

Examining Adam’s State

For our frozen encoder, the maximum values in each state tensor were:

	Encoder	Decoder
exp_avg	1.96e+05	1.70e+06
exp_avg_sq	0	1.18e+11

Wait, WHAT?! The encoder’s exp_avg_sq is zero despite having momentum accumulated in exp_avg.

This feels mathematically impossible… The second moment (exp_avg_sq) is zero despite non-zero gradients. Since exp_avg_sq stores squared gradients, it should NEVER be zero if gradients are non-zero.

And if it truly were zero, we’d see massive weight updates.

param_update = lr * exp_avg / (sqrt(exp_avg_sq) + ε) 
             = 0.001 * 1.96e5 / (sqrt(0) + 1e-8)
             = 196 / 1e-8
             = 1.96e10  # <-- HUGE!

This would be huge! Yet we see NO updates… this paradox points to a deeper issue.

Testing Hypotheses

Could it be bias correction?

Adam uses bias correction to counteract zero initialization. Having previously encountered subtle training issues due to Adam bias initialization bugs, I wondered if the correction might be broken here. 💡If you haven't been hurt by a bias correction bug before, check out these examples to learn the importance of getting this step right!

Recall, the bias correction is simply making our effective beta values dependent on the step index, so if the issue has to do with bias correction, it might have some relation to our beta parameters or step index.

I tested with different beta values, at different steps, and even beta_2=0 (which bypasses the exponential average entirely, making exp_avg_sq = grad**2 directly). The encoder’s exp_avg_sq still stayed zero, making bias correction seem less likely as a culprit.

Plus, exp_avg updated correctly despite using the same bias correction mechanism. So maybe something else is preventing exp_avg_sq from updating.

Is it a precision issue?

My largest gradients were big (1e6), and squared that’s 1e12. While that is quite large, it shouldn’t overflow in float32. However, I’ve also been hurt by precision bugs beforeFloating point precision issues have a fun habit of causing silent failures/degradations like this one (where it completes but produces incorrect values). Always worth checking, even when it seems unlikely., so I had to try it anyway.

I moved everything to float64… AND IT STARTED WORKING!

😵‍💫

Wait... how could this possibly be a precision issue?!

I asked Claude to help me understand the situation & was told there are intermediate calculations in Adam that might overflow...

...but I couldn't find these mysterious intermediates in the code. And how would an overflow produce exact zeros instead of inf/NaN? Maybe we divide by the inf somewhere? Or there's an error correction step? Or we're underflowing? But that shouldn't give ALL zeros?!?!

...Going to fp64 DID fix it though, and LLMs probably know PyTorch better than I do, so maybe I'm missing something obvious? But where was this secret intermediate? I couldn't find it anywhere...

so now what???

After a few more minutes of spiraling You're probably not reading this for the mid-debugging-self-doubt, but every debugging adventure has a spiraling moment (at least for me) so feels disingenuous to skip this step. And maybe one of these theories could've actually been correct! , I realized something: when I switched to float64, I also had to switch from MPS (Apple Silicon GPU) to CPU, since MPS doesn’t support float64. I’d changed two variables at once.

Testing with float32 on CPU… the weights update!!

💡

Turns out, precision wasn't the culprit, it was device-specific! The exact same float32 code updates weights on CPU but fails on MPS. This was progress: same code, same datatypes, but different devices meant different implementations—and different bugs.

﹡ This is progress!!

﹡ Note to self… simpler explanations are more likely correct- even (and especially!) when LLMs confidently assert complicated theories that are hard to understand / verify

﹡ Now I just need to figure out why the bug only occurs with MPS

Device-Specific Differences

Why the Same Operation Behaves Differently on Different Chips

PyTorch’s device abstraction lets you write the same code and run it on CPUs, GPUs, and even Apple Silicon. It feels like the same computation is running everywhere — but under the hood, each device has its own entirely separate implementation.

When you call a tensor operation like matmul, PyTorch looks at the tensor’s metadata (e.g. device, dtype, shape) and dispatches to a specialized kernel: a device-specific, highly optimized implementation tailored for that particular hardware backend.

Understanding Apple's GPU Stack and "Kernel" Terminology

Apple’s GPU Stack:

Metal - Apple’s low-level graphics/compute API (like CUDA for NVIDIA)
MPS (Metal Performance Shaders) - High-level optimized functions built on Metal (like cuDNN for CUDA)
PyTorch’s MPS backend - PyTorch’s integration that uses both Metal directly and MPS functions

On “Kernel” Terminology:

Typically, “kernel” refers to low-level GPU code that runs directly on hardware: functions that explicitly manage parallelism across thousands of GPU cores, handle device memory allocation, and are written in chip-specific languages like CUDA or Metal Shading Language.

However, PyTorch seems to also use “kernel” to describe a higher-level abstraction: the framework’s implementation code (C++, Objective-C++, or CUDA files in the native/ directory) that handles specific operations for specific backends. These PyTorch kernels sit above the hardware level- they might call optimized libraries like MPS or cuDNN (which then use those low-level GPU kernels underneath), or they might contain hand-written GPU code.

In this post, we end up primarily exploring PyTorch kernels (e.g. the C++/Objective-C++ code in BinaryOps.mm that orchestrates MPS operations) rather than the Metal compute shaders executing on GPU cores beneath them.

I was surprised these higher-level implementations are also called “kernels” and maybe I have just confused my terminology here but I didn’t have a better name for them so I tried to mostly use “PyTorch kernel” or just “operation” to describe them, though the terminology does get blurry in places.

So when you write something like result = tensor_a @ tensor_b, you’re not invoking a universal multiply function. PyTorch uses the tensors’ metadata to select a device- and dtype-specific kernel that performs the actual computation.

Multiplying two tensors on the CPU uses a completely different kernel than on MPS or CUDA. Even on the same device, changing the dtype or layout can trigger a different kernel. PyTorch maintains a large set of these implementations to support all the combinations.

We’ll see exactly how this dispatch system works in C++ later when we dive into the source code. For now, the important point is: even with identical Python code different tensor metadata → different kernel code → different efficiency / bugs.

In my case, because I’m running this on my M3 MacBook Pro, I’ m using MPS (Metal Performance Shaders), which is the GPU backend for Apple Silicon. While it feels a bit crazy to assume that my training plateau is due to an internal kernel-level bug, it’s a bit less unreasonable with MPS as it’s newer and less mature than the CPU and CUDA backends. (And honestly, most people training/debugging ML models are not doing it on their MacBooks.)

Why Does Only the Encoder Hit This Bug?

The Adam bug appears when working with the encoder on MPS. What makes the encoder different from the decoder that would trigger different behavior?

I tested everything I could think of that might differentiate the two tensors:

Different gradient scales
Dense vs sparse gradient patterns
Removing decoder-specific gradient transformations
Making encoder and decoder gradients statistically identical

Nothing helped. Even when both tensors had similar gradient statistics, only the encoder’s exp_avg_sq stayed frozen. The difference wasn’t in the values of the tensor - something else about the encoder tensor itself was triggering the bug.

What properties does a PyTorch tensor even have? I asked Claude what attributes could differ between two tensors and checked them one-by-one:

	Encoder	Decoder	Same?
Device	mps:0	mps:0	✓
Dtype	float32	float32	✓
Shape	[1536, 384]	[384, 1536]	❌
Requires_grad	True	True	✓
Stride	(1, 1536)	(1536, 1)	❌
Contiguous	False	True	❌

Three differences! The encoder and decoder have different shapes (they’re transposes of each other)PyTorch's nn.Linear stores weights as [out_features, in_features], so the encoder (384→1536) has shape [1536, 384] and the decoder (1536→384) has shape [384, 1536]., different stride patterns, and different contiguity. These properties are all related (more on that below).

The shape difference itself can’t cause different behavior (PyTorch operations handle any shape). But contiguity? That’s a low-level memory detail that could be relevant. Maybe the MPS Adam bug only affects non-contiguous tensors? Worth a shot:

model.encoder.weight.data = model.encoder.weight.contiguous()
optimizer.step()
# Encoder updates!! ✓

IT WORKS! But why?

Tensor Memory Layouts

What Does “Contiguous” Even Mean?

Your computer’s memory is just a flat, 1D array of bytes, but tensors represent multi-dimensional grids. When you index tensor[i, j], PyTorch needs to find that element in the flat memory. The tensor’s stride tells it how to do this conversion (and the exact amount you jump between elements depends on the dtype and how much memory each element takes up).

Think of stride as navigation instructions: “to get from one row to the next, skip this many elements.” By default, memory is stored row-wise—each row is stored sequentially, then the next row comes after. If you read through a row, you skip over 1 element at a time; to go to the next row, you move row-length elements over. (This is why going across a row is faster than going down a column.)

However, the memory layout doesn’t have to match the logical layout we use to think about the tensor. We can change how the user views the tensor without moving any data! For example, when we run transpose (.T), we don’t need to move around any data—we just change the stride!

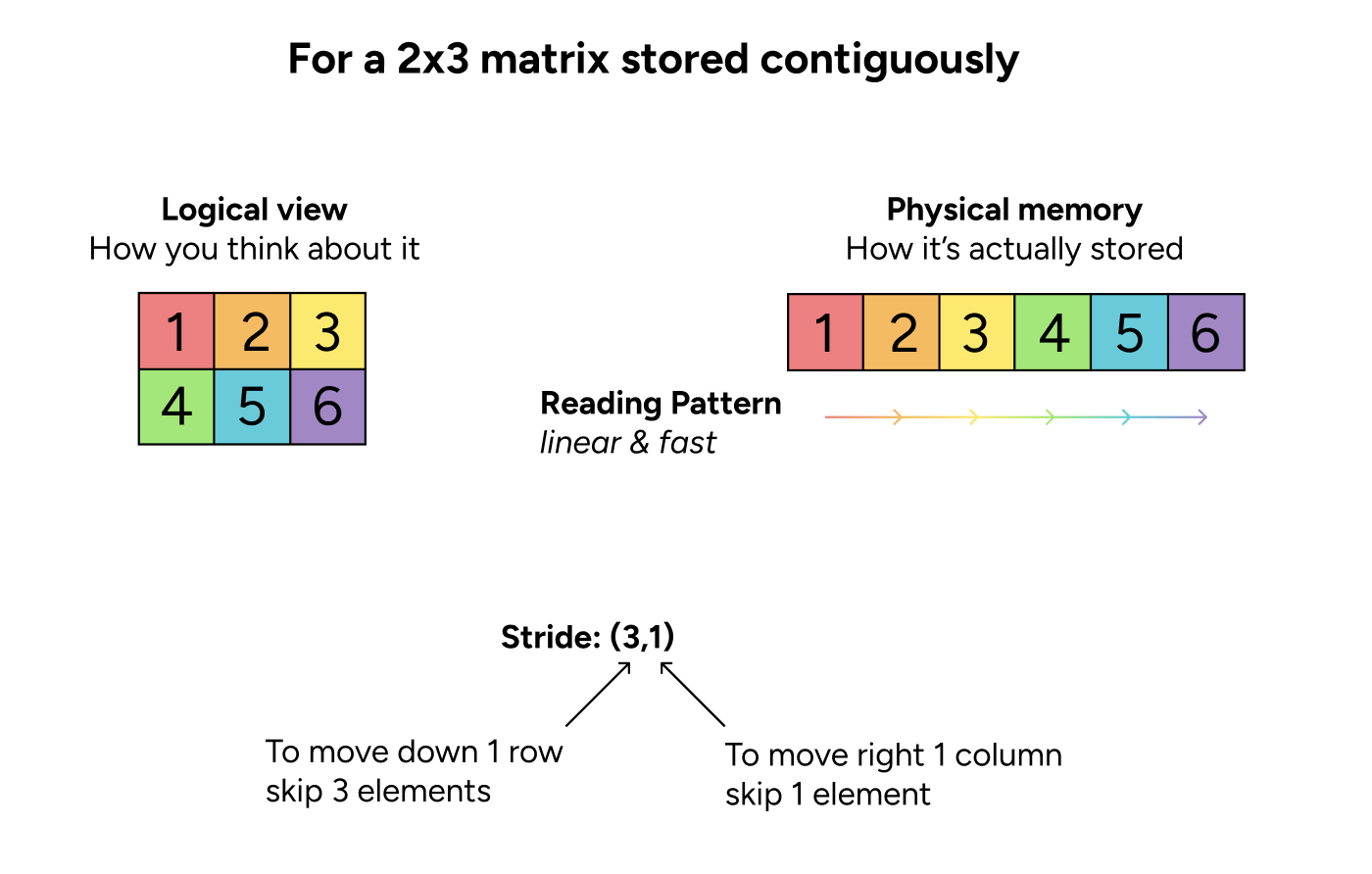
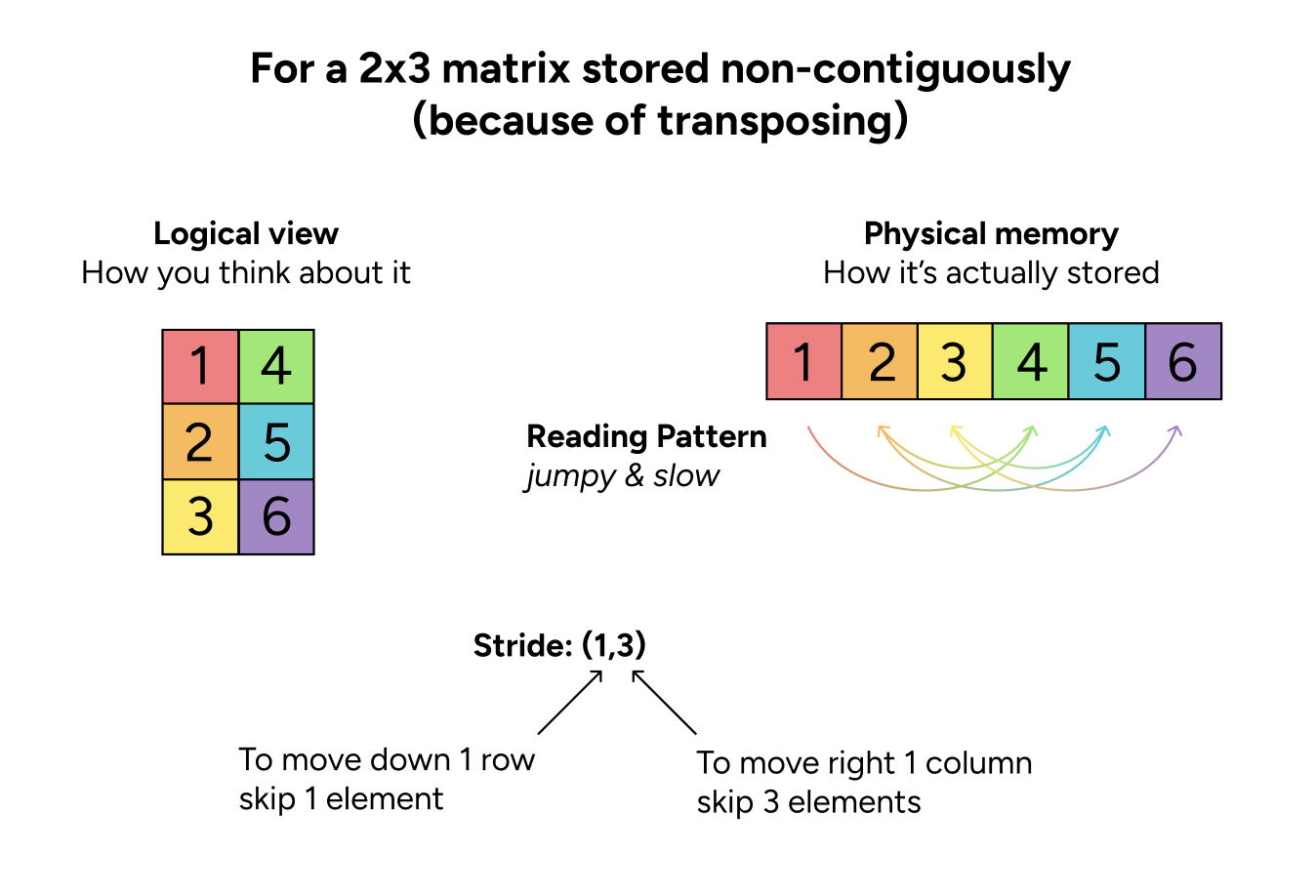
As we see in the images, reading all the elements row-by-row in the contiguous tensor is easy and linear, but the same row-wise pattern in the non-contiguous tensor is much jumpier. This jumping pattern makes the tensor “non-contiguous.”

While there’s only one way for a tensor to be contiguous (the “natural” layout), there are many ways to become non-contiguous. By default, tensors are initialized as contiguous, but operations like slicing (tensor[::2, :]), reshaping, and dimension reordering (permute) can all create different non-contiguous stride patterns.

Why design tensors this way? Wouldn’t it be simpler to always keep data in the “natural” contiguous layout? The answer is performance: by just adjusting the tensor’s metadata, operations like transpose, slice, and reshape can be nearly instant— no data movement or memory allocation required. Keeping everything contiguous would mean expensive copying every time you reorganize dimensions.

How My Encoder Became Non-Contiguous

Looking at the weight initialization code:

self.encoder.weight.data = self.decoder.weight.T.clone()

The .T creates a non-contiguous view, and .clone() preserves the stride pattern.

Why does .clone() preserve stride patterns?

At first this felt counterintuitive to me- if we’re already paying the cost to copy the data (the whole point of non-contiguous layouts is to avoid copying), why not copy it into the “better” contiguous layout?

But this actually makes sense from a design perspective: .clone() should create an exact copy with all properties preserved, including memory layout. The tensor might be non-contiguous for a reason—maybe you’re about to transpose it back, or the layout is optimized for some operation. Silently reorganizing memory would be surprising behavior. (The optional torch.memory_format argument, which defaults to torch.preserve_format, makes this choice explicit.)

As a bonus, preserving the layout is also faster. Even though both include new memory allocation and moving data, reorganizing it still slows things down:

x_t = x.T  # Start with non-contiguous
y_noncontig = x_t.clone()              # Preserves non-contiguous (1.919ms)
y_contig = x_t.clone(memory_format=torch.contiguous_format)  # Force contiguous (4.401ms)

Okay so we now know this initialization is why only the encoder is non-contiguous, and thus why only the encoder has training issues!

While I could just call .contiguous() on my encoder, declare victory, and get back to the research this bug was blocking me from doing… I felt like I was just scratching the surface of this bug and I feared it would haunt me until I fully figured out WHAT happened and WHY.

🔎

Why does a non-contiguous encoder weight cause zero second moment and no parameter updates with Adam on MPS??

Identifying the Broken Operations

What Operations Does Adam Use?

When Adam updates parameters, what operations does it perform? Let’s look at PyTorch’s Adam implementation.

Fair warning: this file is over 1000 lines! To find what we need, search for where exp_avg and exp_avg_sq are defined and updated.

Here are the critical lines (lines 101, 391-407):

# State initialization (line 101)
state["exp_avg"] = torch.zeros_like(param, memory_format=torch.preserve_format)
state["exp_avg_sq"] = torch.zeros_like(param, memory_format=torch.preserve_format)

# ... [300 lines of setup and parameter group handling] ...

# First moment update (line 391)
exp_avg.lerp_(grad, 1 - beta1)

# Second moment update (line 392)
exp_avg_sq.mul_(beta2).addcmul_(grad, grad, value=1 - beta2)

# ... [bias correction calculations] ...

# Parameter update (line 407)
param.addcdiv_(exp_avg, denom, value=-step_size)

Look at that initialization! memory_format=torch.preserve_format means the state tensors inherit their stride pattern from param. So when our encoder weight is non-contiguous, both exp_avg and exp_avg_sq are also non-contiguous.

But they’re BOTH non-contiguous - so why does only one break?

Well, while they both are computed via addition and multiplication, they don’t use the exact same operations to perform this. Any of these operations could be a suspect, so let’s test each one individually!

For operations like output.addcmul_(input1, input2), the output tensorIn PyTorch, when a function name ends with an underscore (like mul_), that indicates that it is performing an in-place operation to modify a tensor directly in memory. Just as different devices can distinct kernels, so can distinctions like these! is modified while input tensors are read from. In our case, we know the output tensor is non-contiguous, so let’s test if that is sufficient to cause our bug.

Testing the Broken Operations

Testing each Adam operation with non-contiguous output tensors on MPS:

Operation	Function	Result
Linear interpolation	`lerp_()`	Updates ✓
Scalar multiply	`mul_()`	Updates ✓
Add + multiply	`addcmul_()`	Stays zero ✗
Add + divide	`addcdiv_()`	Stays zero ✗

‼️

Found it! addcmul_() and addcdiv_() both fail silently when writing to non-contiguous outputs on MPS.

Interestingly, input contiguity doesn’t matter, only the output! Whether grad, exp_avg, or denom are contiguous makes no difference. The bug is purely in how these kernels write to non-contiguous output buffers.

The broken operations aren’t producing zeros or NaNs. They’re simply not modifying the output tensor at all. This wasn’t immediately obvious since exp_avg_sq was initialized to zeros, making “stays at zero” and “never updates” look identical. But testing with a non-zero, non-contiguous output tensor confirms that after calling addcmul_ or addcdiv_, the values remain unchanged. No update happens.

Yet timing shows MPS is doing substantial work. Non-contiguous operations take >2x longer than contiguous ones, proving the kernels are computing something, yet those results never make it to the output tensor. On CPU, each of these operations work correctly regardless of memory layout. This is purely a MPS-specific bug.

With the broken operations identified, we can trace the complete chain of events that triggers our failure:

Putting the Pieces Together

Show the complete bug chain in code

Step 1: Initialization

# Creates non-contiguous encoder weight (stride: 1, 1536)
encoder.weight = decoder.weight.T.clone()

Step 2: Adam State Creation

# Both state tensors inherit non-contiguous layout from param
state["exp_avg"] = zeros_like(param, memory_format=torch.preserve_format)
state["exp_avg_sq"] = zeros_like(param, memory_format=torch.preserve_format)

Step 3: Optimization Loop

First moment update:

exp_avg.lerp_(grad, 1-beta_1)  # ✓ Works fine

Second moment update:

exp_avg_sq.mul_(beta_2)                        # ✓ Works fine
exp_avg_sq.addcmul_(grad, grad, 1-beta_2)      # ✗ No update - stays zero!

Step 4: Parameter Update

# Should update param, does nothing, leading to silent failure
param.addcdiv_(exp_avg, denom, value=-step_size)  # ✗ No update!

If only exp_avg_sq.addcmul_() failed, the zero exp_avg_sq would produce massive weight explosions (update = lr × exp_avg / √(ε)), making the bug immediately obvious. But param.addcdiv_() also failed, producing no updates at all!

The second bug masked the first, creating a silent failure: the spookiest type of error. The model appeared to be learning (the decoder was training normally), but progress stalled because the encoder stayed frozen. A subtle plateau that looked exactly like a hyperparameter issue 🙃

Side note: Why did forward and backward passes work fine with non-contiguous weights?

If non-contiguous tensors can cause operations to silently fail on MPS, why didn’t the forward pass or backward pass break?

The forward and backward passes for F.linear use matmul for their matrix multiplications, which handle non-contiguous tensors correctly on MPS. Testing confirms that both matmul (the @ operator) and F.linear work correctly with non-contiguous input tensors and non-contiguous weight matrices on MPS, including during the backward pass where gradients flow through non-contiguous weights without issues.

The bug is specific to the fused in-place operations that Adam uses for state updates: addcmul_ and addcdiv_. These operations fail silently when writing to non-contiguous output tensors, while other in-place operations like lerp_ and mul_ work correctly.

While we have made so much progress on this case, we’re still not done yet!!

Remaining Question

🔍

Why do addcmul_ and addcdiv_ fail to update non-contiguous outputs while mul_ and lerp_ work fine?

Inside the Kernel Implementation

To understand why some operations work and others don’t, I needed to look at PyTorch’s source code for the buggy kernels.

While I normally trace through a Python codebase by jumping to definitions in my IDE, that doesn’t work with tensor.addcmul_(). When you call this function, there’s no Python source code executing - instead, Python immediately jumps into compiled C++ code for performance. And since PyTorch ships this as a pre-compiled binary, I can’t see that C++ implementation.

How can Python call C++ functions? (a brief aside on bindings)

How can a Python tensor object have methods that execute C++ code? I skipped over this earlier but even though I know PyTorch isn’t the only framework to do this and everything is just machine code if you zoom in close enough… it still feels a bit magical to casually call another language.

The explanation is Python bindings.

When you install PyTorch, you’re not just getting Python files. You’re also getting compiled C++ libraries (.so files on Linux/Mac, .dll on Windows) that contain the actual mathematical operations. The Python part is essentially a wrapper that:

Takes your Python arguments (tensor, other_tensor, etc.)
Converts them to C++ data structures
Calls the appropriate C++ function
Converts the C++ result back to a Python tensor
Returns it to your Python code

PyTorch uses pybind11 to automatically generate this wrapper code. For example, the C++ function signature:

Tensor& addcmul_(Tensor& self, const Tensor& tensor1, const Tensor& tensor2, const Scalar& value)

Gets automatically wrapped so you can call it from Python as:

tensor.addcmul_(tensor1, tensor2, value=1.0)

This is why PyTorch operations are fast despite being called from Python - the heavy lifting happens in optimized C++ code, with Python just handling the interface.

And as we discussed earlier, PyTorch dispatches based on tensor metadata, so there isn’t just one implementation - there are device-specific kernels for CPU, CUDA, MPS, etc. Since my PyTorch installation just has the compiled binary files, to investigate the actual implementations, we need to clone PyTorch’s repository.

PyTorch’s Dispatch System

All kernels are listed in an operation registry - a YAML file that maps operation names (like addcmul_) to their tensor-specific C++ implementations. In practice, when PyTorch is compiled (normally done before you install it), this registry is used to automatically generate hundreds of scripts that do the actual dispatching based on the patterns described here, but if we just want to understand what kernel our tensor is calling, we can look through the registry.

Searching for “addcmul_” in the registry native_functions.yaml:

- func: addcmul_(Tensor(a!) self, Tensor tensor1, Tensor tensor2, *, Scalar value=1) -> Tensor(a!)
  # our addcmul_ function just points us to the yaml for addcmul.out
  structured_delegate: addcmul.out

# The function addcmul_ points to:
- func: addcmul.out(...)
  dispatch:
    CPU, CUDA: addcmul_out
    MPS: addcmul_out_mps  # Different function for MPS!

Now that we have the device-specific operation names, we can search them in the PyTorch repo within the mps implementations, and we find our implementation for addcmul_out_mps in PointwiseOps.mm. Upon a first skim of the code, I realized I had no clue how to read the MPS codebase. There were too many unknown variables and constructs, and I wasn’t sure what to look for in this implementation. I’d written a CUDA kernel before, and was pretty good with C about a decade ago, but as turns out, neither of those helped here :(

Comparing Broken vs Working Implementations

Rather than trying to decode unfamiliar code in isolation, I’d find something similar that works correctly and compare the two. mul_ was the perfect comparison since both are simple element-wise in-place operations. The registry pointed me to binaryOpTensor in BinaryOps.mm.

Now I had my comparison:

Broken: addc_mul_div_out_mps in PointwiseOps.mm (used by addcmul_)
Working: binaryOpTensor in BinaryOps.mm (used by mul_)

I opened both side-by-side, scanning specifically for differences in how they handle the output tensor. My experiments had already narrowed the search: I knew both operations were computing something (timing proved that), so the bug had to be in how results get written back to non-contiguous outputs. Look for anything related to contiguity checks or special output handling.

Broken version (addcmul_):

static void addc_mul_div_out_mps(..., Tensor& output, ...) {
  // ... setup code ...
  Placeholder outputPlaceholder = Placeholder(output);
  runMPSGraph(...);
  // That's it - no additional handling
}

Working version (mul_):

static void binaryOpTensor(..., Tensor& output, ...) {
  // ... setup code ...
  
  bool needsCopyToOutput = !output.is_contiguous();
  if (needsCopyToOutput) {
    // Create temporary contiguous tensor
    output = at::empty(...);
  }
  
  Placeholder outputPlaceholder = Placeholder(output);
  runMPSGraph(...);
  
  if (needsCopyToOutput) {
    output_.copy_(output);  // Copy results back!
  }
}

The working version explicitly checks !output.is_contiguous() and adds extra handling: it creates a temporary contiguous tensor, runs the operation, then copies results back. The broken version just passes the output directly to Placeholder and calls it a day.

But this raises a new question: if non-contiguous memory layouts need this kind of explicit handling, why doesn’t addcmul just crash or throw an error instead of silently failing?

The Memory Conversion Problem

The answer lies in understanding what Placeholder does. PyTorch tensors and Metal (Apple’s GPU framework) use different memory formats, so PyTorch needs a converter when running operations on Apple Silicon. Placeholder handles this conversion - it takes PyTorch tensors and wraps them in Metal-compatible buffers, handles different data types, manages memory layouts, and sets up the compute pipeline.

For most tensors, this conversion is straightforward. But for non-contiguous tensors, Metal can’t work with the scattered memory layout directly. Looking at the Placeholder code:

if (!src.is_contiguous()) {
    _tensor = src.clone(MemoryFormat::Contiguous);  // Create contiguous copy
    srcBuf = getMTLBufferStorage(_tensor);          // Point Metal to the copy
}

When Placeholder encounters a non-contiguous tensor, it automatically creates a contiguous copy and points Metal to that copy instead. This happens transparently - the broken kernels have no idea they’re working with a temporary.

This automatic copying is perfect for input tensors - Metal reads from the copy, computation proceeds normally, and nobody cares what happens to the temporary afterward.

But it’s disastrous for output tensors where the goal is in-place editing. The computation succeeds and writes results to the temporary copy, but those results never make it back to the original tensor that’s supposed to be updated.

Why is this MPS-Specific?

If non-contiguous tensors are so problematic, why do CPU and CUDA backends handle them fine?

CPU: Can handle arbitrary strides natively. When iterating through a non-contiguous tensor, the CPU just follows the stride pattern—jumping around memory is slower than sequential access, but it works correctly.

CUDA: NVIDIA’s CUDA framework has always supported strided memory access in kernels. Operations can read/write to non-contiguous layouts directly, though with some performance penalty.

MPS: Apple’s Metal Performance Shaders framework initially didn’t support strided access. Kernels expected contiguous memory layouts, period. This forced PyTorch to implement the gather-scatter workaround pattern we saw in the working kernels.

The bug occurred because some MPS operations implemented this workaround (like mul_), while others didn’t (like addcmul_). The abstraction (Placeholder) that was supposed to hide this complexity actually made it worse by silently copying outputs without a way to copy results back. Although as we’ll learn later this has been improved in newer Mac Operating Systems.

The Complete Bug Mechanism

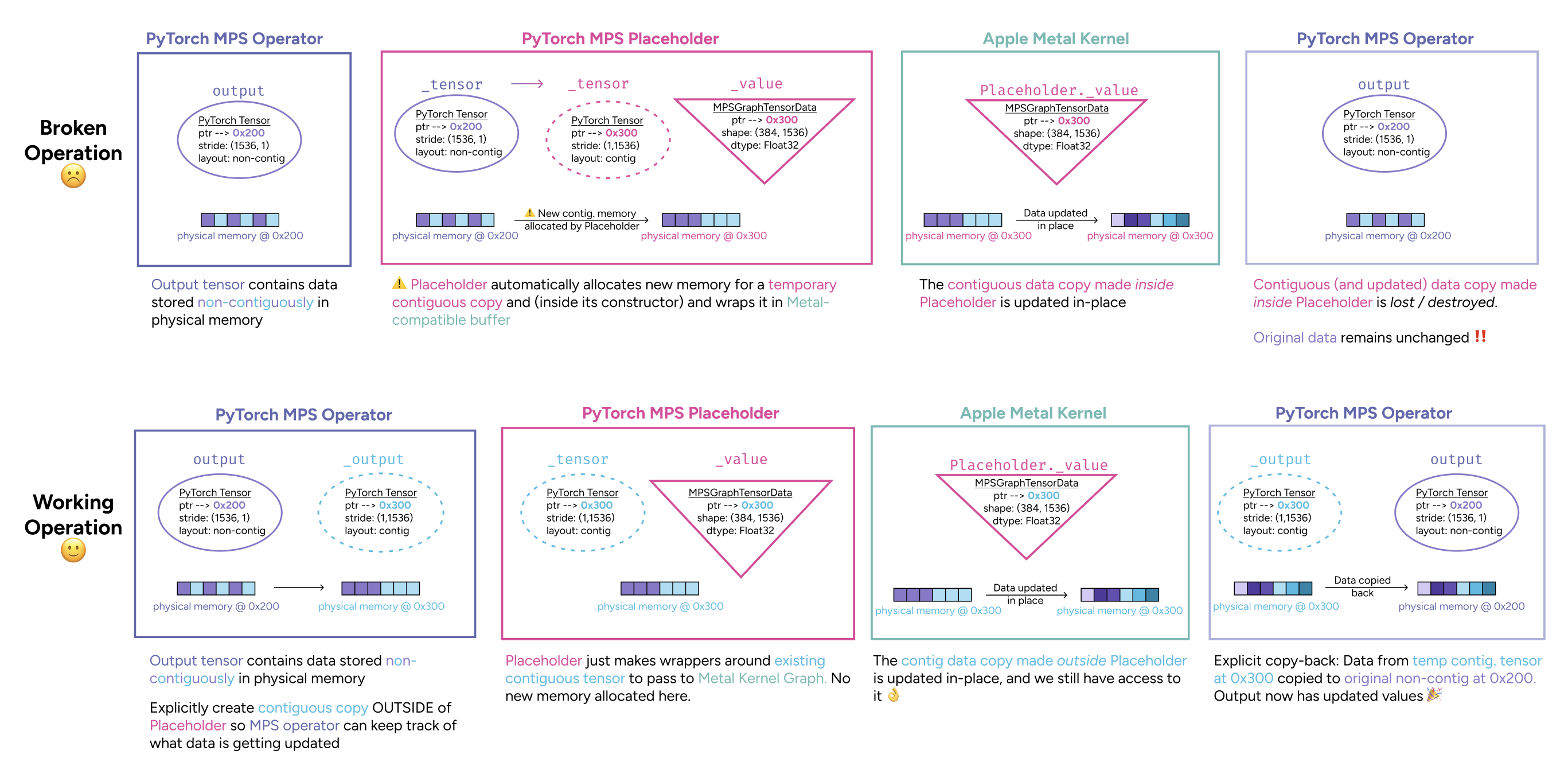
The broken kernels work perfectly with contiguous tensors and silently fail with non-contiguous ones. The working kernels detect this situation and add an explicit copy-back step to move results from the temporary to the original tensor.

The Fix

Understanding the bug made the solution clear - apply the same pattern that working kernels use:

Tensor output = output_;
bool needsCopyToOutput = false;
 
if (!output_.is_contiguous()) {
 output = at::empty(...); // Create contiguous buffer WE manage
 needsCopyToOutput = true;
}
 
@autoreleasepool {
 Placeholder outputPlaceholder = Placeholder(output);
 runMPSGraph(...);
}
// No copy-back - results vanish when Placeholder dies
 
if (needsCopyToOutput) {
 output_.copy_(output); // Copy results back
}

I tested this locally and it worked! The encoder weights finally updated and the model trained successfully 🎉🎉

You can see the complete reproduction, debugging experiments, fix at https://github.com/ElanaPearl/pytorch-mps-noncontiguous-bug.

Case Closed

A Lesson in Version Control

While editing a Python package just involves installing your locally editable version of the code instead of the default package, to test my PyTorch fix, I had to re-build it all locally, which was more work than expected and also made me acutely aware that this whole time I was working on PyTorch v2.2.1I was working on a research codebase with dependency conflicts that blocked upgrading PyTorch. Common enough situation, but lesson learned: always check versions early in debugging, even if you can't immediately update! (as this fact made it difficult to build and I had to downgrade things like CMake and deal with weird version conflicts to even build this older PyTorch).

Checking the latest version revealed the bug was already fixed in v2.4, patched by an ML engineer at Apple last year using almost the exact same approach I’d used.The official fix uses slightly different syntax; but the same core pattern: detect non-contiguous output, create a contiguous temporary buffer, perform the computation, then copy results back to the original tensor. This updated code even informed me that in macOS 15+, MPS now handles non-contiguous tensors natively! In macOS 15, Apple added native strided array support to MPSGraph via the arrayView API (see WWDC 2024 session at timestamp 13:41). Instead of the gather-scatter workaround, Metal can now read/write directly from non-contiguous memory using stride metadata. This means on macOS 15+, PyTorch can skip the manual copy workarounds entirely. The performance gap between contiguous and non-contiguous tensors is now much smaller, though contiguous is still faster due to better cache utilization.

🤦‍♀️

While I now felt silly for diving so deep on an already-fixed bug, the process was still very fun, educational, and so worth the effort.

In hindsight, I maybe could've tried upgrading PyTorch earlier...

...But as it turns out, the story wasn't over just yet!

The Pattern Strikes Again

While writing this up, I added some more tests for my kernel fix to confirm it really worked, and one of the tests failed! I looked into it more and realized I’d stumbled upon the same failure pattern in the random_ operation (in the most up-to-date PyTorch this time!)

Turns out, all random in-place operations (normal_, uniform_, exponential_, random_, bernoulli_) silently fail when called on non-contiguous tensors on MPS.

x = torch.zeros(10, 10).T  # Non-contiguous
x.normal_()  # Should fill with random values
print(x.max())  # Prints 0.0 - the operation silently failed!

Yet again, the operations complete without error, but the tensor remains unchanged—the kernel computes random values into a temporary contiguous buffer but never copies them back.

Having just traced through this exact bug pattern, I recognized it immediately and knew exactly how to fix it. Filed an Issue and made a PR applying the same solution.

I suspect there are other similar bugs lying around, as none of these fixes actually address the underlying quirk that the Placeholder abstraction itself is problematic when used with output tensors.

The core issue: Placeholder’s constructor silently creates a temporary contiguous copy for non-contiguous tensors, but it has no way to know if it’s wrapping an input (where the copy is fine- we just read from it) or an output (where the copy is broken- results get written to it then lost). This means every single operation that uses Placeholder for outputs must manually implement the same workaround pattern or else it has this silent failure:

// Every MPS operation must remember to do this:
bool needsCopy = !output.is_contiguous();
Tensor temp = needsCopy ? at::empty(...) : output;
@autoreleasepool {
    Placeholder p(temp);
    runGraph();
}
if (needsCopy)
  output.copy_(temp);

This is a leaky abstractionA "leaky abstraction" is when an abstraction that's supposed to hide implementation details forces you to understand and work around those details anyway. Placeholder is supposed to abstract Metal buffer management, but its internal copying leaks through, forcing every caller to manually handle non-contiguous outputs. See Joel Spolsky's The Law of Leaky Abstractions for the canonical explanation.: the internal implementation detail that “Placeholder makes temporary copies” has leaked out to every caller, making it each operation’s responsibility to work around. A better design would be:

Placeholder knows input vs output: Pass a flag so Placeholder can handle the copy-back itself
Separate abstractions: Different wrapper types for inputs (InputPlaceholder) and outputs (OutputPlaceholder)
Make the temporary explicit: Don’t hide the copy inside Placeholder—make callers explicitly create and manage contiguous temporaries (this is what I used in the fixes for addcmul_/addcdiv_/the random ops)

The good news: macOS 15+ Metal now handles non-contiguous tensors natively, making this entire issue obsolete for newer systems. But for anyone on older macOS versions or maintaining PyTorch’s MPS backend, this abstraction continues to cause issues.

So ideally, the Placeholder class would be redesigned to handle output tensors correctly by default, but given that the hardware is moving to handle this natively anyway, the pragmatic fix is probably just to audit and patch the remaining operations using the established pattern.

Practical Takeaways for Your Code

Performance Considerations

Even with the code fixes, non-contiguous tensors on MPS involve: Allocate temporary buffer -> Copy to contiguous layout -> Compute -> Copy back. Making tensors contiguous once at initialization avoids thousands of copies during training! And even if your OS can avoid making this temporary contiguous copy, it is still slower to operate on non-contiguous memory if you will be using it many times.

When to Call .contiguous()

# When to call .contiguous() - General Principles

# 1. After operations that change memory layout:
x = tensor.transpose(0, 1)  # Non-contiguous
x = tensor.view(-1)          # Might fail if non-contiguous!
x = x.contiguous().view(-1)  # Safe

# 2. Before operations that might not handle strides:
# - Custom CUDA/Metal kernels  
# - Newer backend features
# - Operations that failed mysteriously on certain devices

# 3. For performance on repeated operations:
weights = init_weights().T   # Used in every forward pass
weights = weights.contiguous()  # Pay copy cost once, not every iteration

# But don't overuse it!
x = x + y  # Creates new contiguous tensor anyway
x = x.contiguous()  # Unnecessary copy!

For MPS specifically: If on macOS <15, make sure all your parameters are contiguous!

What I Learned

Isolate to specific, measurable symptoms. The most standard advice and for such good reason. Everything got easier once I had a concrete target: “exp_avg_sq stays at zero” is infinitely more debuggable than “the loss plateaus mysteriously.” Once I had a specific symptom, I could strip away components and test the minimal case that triggered it.

When debugging tensor issues, check metadata not just values. I was checking for NaNs, visualizing weights, inspecting gradients—all focused on the numbers inside tensors. The actual problem was the tensor’s stride pattern. Device, dtype, contiguity, memory layout—these aren’t just performance details, they can cause silent correctness bugs. tensor.is_contiguous() is now part of my debugging checklist.

When I’m confused, I might have changed two things—or there might be two bugs. Switching to fp64 “fixed” it, but I’d also switched from MPS to CPU. Untangling that revealed the real culprit. And exp_avg_sq staying zero should have caused explosions, but the parameter update also failed—one bug perfectly masked the other.

Documentation makes more sense when I need it. I’d skimmed PyTorch internals docs before and nothing stuck—dispatch systems, stride patterns, kernel implementations all felt overwhelming. But once I had to understand how addcmul_ dispatches to MPS kernels, everything clicked. Now PyTorch feels less like a black box. And when I hit the random ops bug weeks later, I wasn’t intimidated—I knew exactly how to trace through the source.

Explore the system before exploring the code. When I needed to debug addcmul_out_mps in unfamiliar MPS code, I ran experiments first: which operations fail? Do they run at all? What triggers the bug? By the time I opened the source, I knew to compare addcmul_ (broken) against mul_ (working) and scan specifically for differences in output handling. Without that context, I’d have been lost in Objective-C++ with no idea what mattered. Also LLMs were very helpful with unfamiliar constructs like MPSGraphTensor or @autoreleasepool, although they’re still less reliable with MPS than more documented frameworks.

Write post-mortems– even for yourself. Forcing myself to explain why I tried each debugging step was as educational as the original investigation. It’s like experience replay in RL: you explore many failed paths, find one that works, then replay that successful trajectory to reinforce the policy. Writing it down builds pattern recognition—when I’m in “situation A”, what hypotheses are worth trying? I’ve written lower-effort debugging debriefs before, but making this one readable for an external audience forced me to articulate why each step made sense, deepening my understanding of what actually worked.

What started as a frustrating research roadblock became a surprisingly fun & educational detour. It forced a closer look at things normally taken for granted: Adam’s momentum mechanics, stride patterns, kernel dispatch. Understanding why each operation behaved differently revealed more about PyTorch’s architecture than typical usage ever does.

If you made it this far, thanks for joining! Hope you had fun and/or learned something & happy debugging!

Special thanks to Nicholas Joseph, Ben Kuhn, Nelson Elhage and Alex Tamkin for giving feedback on this 💜